|
|
Liebermann, D. G., Krasovsky, T., & Berman, S. (2008). Planning maximally smooth hand movements constrained to nonplanar workspaces. J Mot Behav, 40(6), 516–531.

Abstract: The article characterizes hand paths and speed profiles for movements performed in a nonplanar, 2-dimensional workspace (a hemisphere of constant curvature). The authors assessed endpoint kinematics (i.e., paths and speeds) under the minimum-jerk model assumptions and calculated minimal amplitude paths (geodesics) and the corresponding speed profiles. The authors also calculated hand speeds using the 2/3 power law. They then compared modeled results with the empirical observations. In all, 10 participants moved their hands forward and backward from a common starting position toward 3 targets located within a hemispheric workspace of small or large curvature. Comparisons of modeled observed differences using 2-way RM-ANOVAs showed that movement direction had no clear influence on hand kinetics (p < .05). Workspace curvature affected the hand paths, which seldom followed geodesic lines. Constraining the paths to different curvatures did not affect the hand speed profiles. Minimum-jerk speed profiles closely matched the observations and were superior to those predicted by 2/3 power law (p < .001). The authors conclude that speed and path cannot be unambiguously linked under the minimum-jerk assumption when individuals move the hand in a nonplanar 2-dimensional workspace. In such a case, the hands do not follow geodesic paths, but they preserve the speed profile, regardless of the geometric features of the workspace.
|
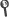
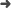
|
|
|
Biess, A., Liebermann, D. G., & Flash, T. (2007). A computational model for redundant human three-dimensional pointing movements: integration of independent spatial and temporal motor plans simplifies movement dynamics. J Neurosci, 27(48), 13045–13064.

Abstract: Few computational models have addressed the spatiotemporal features of unconstrained three-dimensional (3D) arm motion. Empirical observations made on hand paths, speed profiles, and arm postures during point-to-point movements led to the assumption that hand path and arm posture are independent of movement speed, suggesting that the geometric and temporal properties of movements are decoupled. In this study, we present a computational model of 3D movements for an arm with four degrees of freedom based on the assumption that optimization principles are separately applied at the geometric and temporal levels of control. Geometric properties (path and posture) are defined in terms of geodesic paths with respect to the kinetic energy metric in the Riemannian configuration space. Accordingly, a geodesic path can be generated with less muscular effort than on any other, nongeodesic path, because the sum of all configuration-speed-dependent torques vanishes. The temporal properties of the movement (speed) are determined in task space by minimizing the squared jerk along the selected end-effector path. The integration of both planning levels into a single spatiotemporal representation simplifies the control of arm dynamics along geodesic paths and results in movements with near minimal torque change and minimal peak value of kinetic energy. Thus, the application of Riemannian geometry allows for a reconciliation of computational models previously proposed for the description of arm movements. We suggest that geodesics are an emergent property of the motor system through the exploration of dynamical space. Our data validated the predictions for joint trajectories, hand paths, final postures, speed profiles, and driving torques.
|
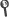
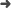
|
|
|
Liebermann, D. G., & Hoffman, J. R. (2005). Timing of preparatory landing responses as a function of availability of optic flow information. J Electromyogr Kinesiol, 15(1), 120–130.

Abstract: This study investigated temporal patterns of EMG activity during self-initiated falls with different optic flow information ('gaze directions'). Onsets of EMG during the flight phase were monitored from five experienced volunteers that completed 72 landings in three gaze directions (downward, mid-range and horizontal) and six heights of fall (10-130 cm). EMG recordings were obtained from the right gastrocnemius, tibialis anterior, biceps femoris and rectus femoris muscles, and used to determine the latency of onset (L(o)) and the perceived time to contact (T(c)). Impacts at touchdown were also monitored using as estimates the major peak of the vertical ground reaction forces (F(max)) normalized to body mass, time to peak (T(max)), peak impulse (I(norm)) normalized to momentum, and rate of change of force (dF(max)/dt). Results showed that L(o) was longer as heights of fall increased, but remained within a narrow time-window at >50 cm landings. No significant differences in L(o) were observed when gaze direction was changed. The relationship between T(c) and flight time followed a linear trend regardless of gaze direction. Gaze direction did not significantly affect the landing impacts. In conclusion, availability of optic flow during landing does not play a major role in triggering the preparatory muscle actions in self-initiated falls. Once a structured landing plan has been acquired, the relevant muscles respond relative to the start of the fall.
|
|
|
|
Biess, A., Flash, T., & Liebermann, D. G. (2011). Riemannian geometric approach to human arm dynamics, movement optimization, and invariance. Phys Rev E Stat Nonlin Soft Matter Phys, 83(3 Pt 1), 031927.
Abstract: We present a generally covariant formulation of human arm dynamics and optimization principles in Riemannian configuration space. We extend the one-parameter family of mean-squared-derivative (MSD) cost functionals from Euclidean to Riemannian space, and we show that they are mathematically identical to the corresponding dynamic costs when formulated in a Riemannian space equipped with the kinetic energy metric. In particular, we derive the equivalence of the minimum-jerk and minimum-torque change models in this metric space. Solutions of the one-parameter family of MSD variational problems in Riemannian space are given by (reparameterized) geodesic paths, which correspond to movements with least muscular effort. Finally, movement invariants are derived from symmetries of the Riemannian manifold. We argue that the geometrical structure imposed on the arm's configuration space may provide insights into the emerging properties of the movements generated by the motor system.
|
|

